Pattern Programs in C

Right Half Pyramid Pattern

The following program displays the right half pyramid pattern:

#include <stdio.h>

int main()
{
    int rows;

    printf("Enter the number of rows: ");
    scanf("%d", &rows);

    for (int i = 1; i <= rows; i++) {
        for (int j = 1; j <= i; j++) {
            printf("* ");
        }
        printf("\n");
    }
}

Output:

Explanation:

The right half pyramid pattern is easiest to print among all. The stars will be displayed according to the row number. The outer loop represents the current row under consideration and the inner loop represents the number of stars to be displayed. 

Assuming the user has entered 3 for the rows variable. Then,

• In the outer loop when i is 1,
  • i  = 1 means we are at row number 1.
  • The stars displayed depend on the value of i. As i is 1, the inner loop will run only 1 time, and therefore only 1 star will be displayed (space separated).
• When i is 2
  • i = 2 means we are at row number 2.
  • The inner loop runs 2 times, therefore, only 2 stars will be displayed.
• When i is 3
  • i = 3 means we are at row number 3.
  • The inner loop runs 3 times, therefore, only 3 stars will be displayed.
• Done

In this way, all the stars according to the current row are displayed.

Left Half Pyramid Pattern

The following program displays the left half Pyramid pattern:

#include <stdio.h>

int main()
{
    int rows;

    printf("Enter the number of rows: ");
    scanf("%d", &rows);

    // i represents the row number (row you are currently at).
    for (int i = 1; i <= rows; i++) {
        // Display row - i white spaces
        for (int j = 1; j <= 2 * (rows - i); j++) {
            printf(" ");
        }

        // Display stars according to the row.
        for (int j = 1; j <= i; j++) {
            printf("* ");
        }
        printf("\n");
    }
}

Output:

Explanation:

To display the right half pyramid with proper whitespaces, we need maximum of (2 * number of rows – 1) columns because in each row, each star is displayed along with a single whitespace (except that last column stars). The following figures depict the same.

In the first row, 8 whitespaces are needed which can be obtained by the formula:

So, in the first row, 8 spaces are needed which is obtained by applying the above formula:  2 x (5 – 1) = 2 x 4 = 8. Similarly, in the second row, 6 whitespaces are obtained by the same formula:  2 x (4 – 1) = 6, and so on.

Let’s evaluate the program for rows = 5. 

• For i = 1 in the outer loop (in the row number 1)
  • The first row needs 1 star and that too in the 9th column.
  • First 8 whitespaces need to be displayed. 
  • To display 8 whitespaces, we need a loop that runs from 1 to 2 * (rows – i). This is because the number of whitespaces in a row depends upon the row where it needs to be displayed. In the first row, we need to display 8 whitespaces, hence 2 * (5 – 1) = 8. 
  • The second inner loop will take care of the number of stars to be displayed. In the first row, only one star along with the whitespace is displayed. 
• For i = 2 (row number 2) in the outer loop,
  • 6 whitespaces are needed.
    • The first inner loop will run 2 * (rows – i) = 2 * (5 – 2) = 6 times means 6 whitespaces will be displayed. 
  • 2 stars needed.
    • The second inner loop will run 2 times, and hence 2 stars will be displayed at the end. 
• For i = 3 (row number 3) in the outer loop,
  • 4 whitespaces are needed.
    • The first inner loop will run 2 * (rows – i) = 2 * (5 – 3) = 4 times means 4 whitespaces will be displayed. 
  • 3 stars needed.
    • The second inner loop will run 3 times, and hence 3 stars will be displayed at the end. 
• For i = 4 (row number 4) in the outer loop,
  • 2 whitespaces are needed.
    • The first inner loop will run 2 * (rows – i) = 2 * (5 – 4) = 2 times means 2 whitespaces will be displayed. 
  • 4 stars needed.
    • The second inner loop will run 4 times, and hence 4 stars will be displayed at the end.
• For i = 5 (row number 5) in the outer loop,
  • 0 whitespaces are needed.
    • The first inner loop will run 2 * (rows – i) = 2 * (5 – 5) = 0 times means 0 whitespaces will be displayed. 
  • 5 stars needed.
    • The second inner loop will run 5 times, and hence 5 stars will be displayed at the end.
• Done

So, in this way, the program will display the required right half pyramid according to the number of rows entered by the user.

Full Pyramid Pattern

The following program displays the full pyramid pattern:

#include <stdio.h>

int main() {
    int rows;
    
    printf("Enter the number of rows: ");
    scanf("%d", &rows);
    
    // for each row of the pyramid
    for (int i = 1; i <= rows; i++) {
        // add whitespaces according to the row.
        for (int j = 1; j <= rows - i; j++) {
            printf(" ");
        }
        
        // print stars according to the row. 
        for (int k = 1; k <= i; k++) {
            printf("* ");
        }
        // go to the next row.
        printf("\n");
    }
}

Output:

Explanation:

To understand the working of the above program, consider the following figure:

From the figure, it is clear that in each row, some number of whitespaces needs to be displayed, and then the stars appear. For example, in the first row, 4 whitespaces need to be displayed and then a single star appears. In the second row, 3 whitespaces and 2 stars. In the third row, 2 whitespaces and 3 stars, and so on. The number of whitespaces is clearly dependent on the row in which they need to be displayed. The formula is rows – i where rows represent the total number of rows of the pyramid and I represents the current row number. You can verify on your own why it works. And, stars are too dependent on the current row.number. If it is row number 3, then 3 stars (along with their whitespaces) will be displayed. If it is row number 5, then 5 stars. 

In the above program, the outer for loop is keeping track of each row. The first inner loop displays whitespaces according to the row number obtained from the outer for loop, and the second for loop will also display stars according to the outer loop. In this way, the pyramid pattern is displayed of any size.

Inverted Right Half Pyramid Pattern

The following program displays the inverted right half pyramid:

#include <stdio.h>

int main() {
    int rows;
    
    printf("Enter the number of rows: ");
    scanf("%d", &rows);
    
    // for each row of the pyramid
    for (int i = 1; i <= rows; i++) {
        // print stars according to the row. 
        for (int k = 1; k <= rows - i + 1; k++) {
            printf("* ");
        }
        // go to the next row.
        printf("\n");
    }
}

Output:

After understanding the previous programs, it is not difficult to understand this program.

Inverted Left Half Pyramid Pattern

The following program displays the left half pyramid pattern:

#include <stdio.h>

int main() {
    int rows;
    
    printf("Enter the number of rows: ");
    scanf("%d", &rows);
    
    // for each row of the pyramid
    for (int i = 1; i <= rows; i++) {
        // print whitespaces according to the row
        for (int j = 1; j <= i * 2 - 2; j++) {
            printf(" ");
        }
        
        // print stars according to the row. 
        for (int k = 1; k <= rows - i + 1; k++) {
            printf("* ");
        }
        // go to the next row.
        printf("\n");
    }
}

Output:

Explanation:

Displaying stars is the same as the program of inverted right half pyramid program. The tricky part is displaying the whitespaces in each row. Let’s take an example Pyramid of 5 rows to understand the process. 

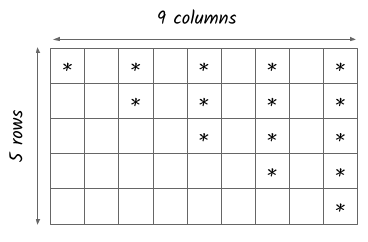
Focus on the last row. In the last row, we need a total of 8 whitespaces. This can be obtained from the row number. As we want 8 whitespaces, we can subtract 2 from 2 times the row number. This gives us 8 for the 5th row, and by using this in the condition of the first inner for loop, we can display 8 whitespaces for the 5th row. The same formula can be used for other rows too. 

The formula for calculating the number of whitespaces for each row:

The rest of the program is easy to understand.

Inverted Full Pyramid Pattern

#include <stdio.h>

int main() {
    int rows;
    
    printf("Enter the number of rows: ");
    scanf("%d", &rows);
    
    // for each row of the pyramid
    for (int i = 1; i <= rows; i++) {
        // print whitespaces according to the row
        for (int j = 1; j <= i-1; j++) {
            printf(" ");
        }
        
        // print stars according to the row. 
        for (int k = 1; k <= rows - i + 1; k++) {
            printf("* ");
        }
        // go to the next row.
        printf("\n");
    }
}

Output:

Explanation:

The program is self-explanatory. 

Hourglass Pattern

#include <stdio.h>

int main() {
    int rows;
    
    printf("Enter the number of rows: ");
    scanf("%d", &rows);
    
    // Inverted full pyramid pattern
    // for each row of the pyramid
    for (int i = 1; i <= rows; i++) {
        // print whitespaces according to the row
        for (int j = 1; j <= i-1; j++) {
            printf(" ");
        }
        
        // print stars according to the row. 
        for (int k = 1; k <= rows - i + 1; k++) {
            printf("* ");
        }
        // go to the next row.
        printf("\n");
    }
    
    // Full pyramid pattern 
    for (int i = 1; i <= rows; i++) {
        // print whitespaces according to the row
        for (int j = 1; j <= rows - i; j++) {
            printf(" ");
        }
        
        // print stars according to the row. 
        for (int k = 1; k <= i; k++) {
            printf("* ");
        }
        // go to the next row.
        printf("\n");
    }
}

Output:

Explanation: 

Hourglass pattern is obtained by playing the inverted full pyramid first and then the full pyramid.

Diamond Pattern

#include <stdio.h>

int main() {
    int rows;
    
    printf("Enter the number of rows: ");
    scanf("%d", &rows);
    
    // Full pyramid pattern 
    for (int i = 1; i <= rows; i++) {
        // print whitespaces according to the row
        for (int j = 1; j <= rows - i; j++) {
            printf(" ");
        }
        
        // print stars according to the row. 
        for (int k = 1; k <= i; k++) {
            printf("* ");
        }
        // go to the next row.
        printf("\n");
    }
    
    // Inverted full pyramid pattern
    // for each row of the pyramid
    for (int i = 1; i <= rows; i++) {
        // print whitespaces according to the row
        for (int j = 1; j <= i-1; j++) {
            printf(" ");
        }
        
        // print stars according to the row. 
        for (int k = 1; k <= rows - i + 1; k++) {
            printf("* ");
        }
        // go to the next row.
        printf("\n");
    }
}

Output:

Explanation:

The diamond pattern is obtained by placing the full pyramid first, and then the inverted full pyramid.

Floyd’s Triangle

#include <stdio.h>

int main() {
    // Variable k will keep track of the natural numbers.
    int rows, k = 1;
    
    printf("Enter the number of rows: ");
    scanf("%d", &rows);
    
    // Floyd's triangle Pattern
    for (int i = 1; i <= rows; i++) {
        // print numbers according to the row. 
        for (int j = 1; j <= i; j++) {
            // display the natural numbers.
            printf("%d ", k);
            k++;
        }
        
        // go to the next row.
        printf("\n");
    }
}

Output:

Explanation:

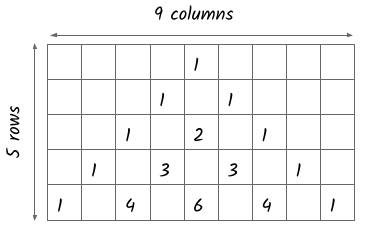
Floyd’s triangle is the triangle of natural numbers where the nth row contains n natural numbers. The following figure shows the Floyd ‘s triangle with 5 rows:

The program will display the Floyd’s Triangle according to the above matrix. Understanding the program is not difficult.

Pascal’s Triangle

Pascal’s triangle has the pattern that each number is the sum of the two numbers just above it. The following figure depicts the same:

We can use the combination formula to find each element of Pascal’s triangle. The following figure shows what each element of the Pascal’s triangle is equivalent to in terms of the combination:

The combination formula:

The following program displays the Pascal’s triangle of any size:

#include <stdio.h>

long int fact(int);
long int nCr(int, int);

long int fact(int n) {
    if (n == 0 || n == 1) return 1;
    else 
        return n * fact(n-1);
}

long int nCr(int n, int r) {
    return fact(n) / (fact(r) * fact(n-r));
}

int main() {
    int rows, k = 1;
    
    printf("Enter the number of rows: ");
    scanf("%d", &rows);
    
    // displaying the Pascal's triangle
    for (int i = 1; i <= rows; i++) {
        for (int j = 1; j <= rows - i; j++) {
            printf(" ");
        }
        
        for (int k = 1; k <= i; k++) {
            printf("%d ", nCr(i-1, k-1));
        }
        printf("\n");
    }
    return 0;
}

Output: